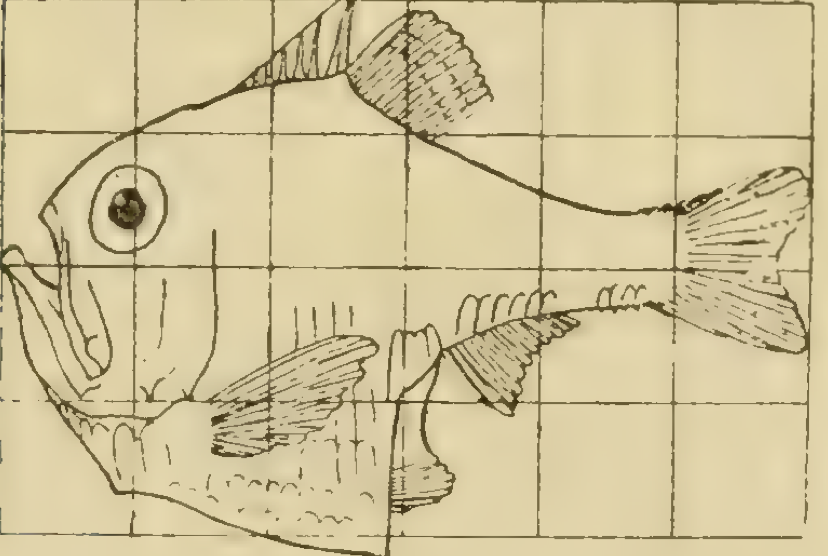
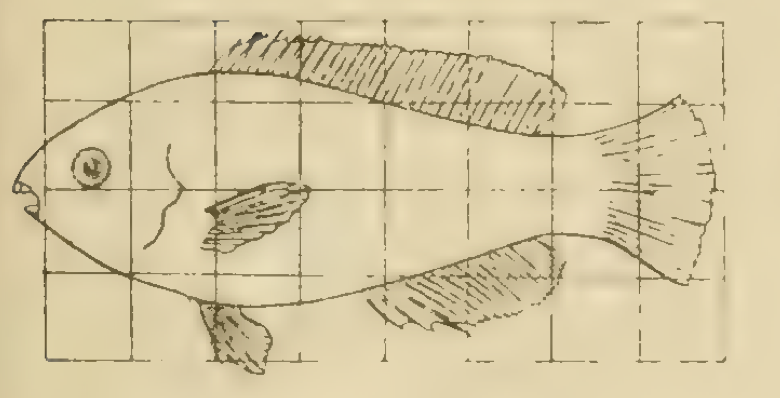
In D’Arcy Thompson’s book ‘On Growth and Form’ he considers how the shapes of related species can be understood using mathematical maps.The underlying idea is that the observed morphological form of an organism (i.e. what you see) is a function of the history of the growth rates of different parts of the organism during development. Although related species can quite different, their shape and size can be sometimes related by quite simple mathematical rules.
In Figure 1 you can see two different species of fish.
Explore mappings via an app
In the app in Figure 2 you can explore mappings similar to those considered by D’Arcy Thompson. The default image initially used is a stock image used in image processing.
- Each map depends on the value of a single parameter.
- A number of different maps are considered.
- You can upload images from your device using the upload button.
- You can download transformed images by right-clicking and saving.
If you save the images in Figure 1 to your computer (right click and ‘Save Image to Download’) you can upload them to the App and explore the effect of the different transformations.
You can also upload your own images (in .png or .jpg format).
#| standalone: true
#| components: [viewer]
#| viewerHeight: 600
from shiny import App, Inputs, Outputs, Session, render, ui
from shiny import reactive
import numpy as np
import matplotlib.pyplot as plt
import skimage as ski
import pyodide
from skimage.transform import SimilarityTransform
from skimage.transform import warp
from skimage.transform import PiecewiseAffineTransform
from skimage.transform import AffineTransform
from skimage.io import imread
import io
from pathlib import Path
from skimage.transform import resize, rescale
def ChooseTransform(transform,im_shape,a,num_disc_points,old_centre):
rows=im_shape[0]
cols=im_shape[1]
src_cols = np.linspace(0, cols, num_disc_points)
src_rows = np.linspace(0, rows, num_disc_points)
src_rows, src_cols = np.meshgrid(src_rows, src_cols)
src = np.dstack([src_cols.flat, src_rows.flat])[0]
dst_rows = src[:, 1]
dst_cols = src[:, 0]
#['Identity','Y stretch','Pinch','Fish eye','Shear','Y squish','Radial']
# add sinusoidal oscillation to row coordinates
#transform='yscaleDarcy299Fig147'
if transform=='Identity':
dst_rows = src[:, 1]
dst_cols = src[:, 0]
elif transform=='Y stretch':
yscaleparam=a
dst_rows = dst_rows*yscaleparam
dst_cols = src[:, 0]
elif transform=='Pinch': #'yscaleDarcy299Fig151':
sc_factor=a
k_x=sc_factor*((dst_cols-cols/2.0)/cols)**1.0+1.0
dst_rows = k_x*(dst_rows-rows/2.0)+rows/2.0
#dst_cols = src[:, 0]
elif transform=='Fish eye': #'yscaleDarcy299Fig149':
dst_rows = ((dst_rows-rows/2.0)*(3.0-a*((dst_cols-cols/2.0)/(cols/2.0))**2.0))+rows/2.0
#dst_cols = (dst_cols-cols/2.0)*(dst_rows-rows/2.0)**2.0+cols/2.0
#dst_cols = src[:, 0]
#dst_cols = src[:, 0]
elif transform=='Shear': #'yscaleDarcy299Fig147':
k_y=-a
dst_cols = dst_cols+k_y*dst_rows
#dst_cols = src[:, 0]
elif transform=='Y squish':
L=np.max(dst_rows)
dst_rows = (np.log(1.0+a*(dst_rows)/L))*L/np.log(2.0)
#dst_cols = src[:, 0]
elif transform=='yscalepower':
L=np.max(dst_rows)
n=a
dst_rows = L*(dst_rows/L)**n
#dst_cols = src[:, 0]
elif transform=='Radial':
dst_rows_max=np.max(dst_rows)
dst_cols_max=np.max(dst_cols)
centre=[cols/2.0,rows/2.0]
radius=np.sqrt((dst_rows-old_centre[0])**2+(dst_cols-old_centre[1])**2)
theta=np.arctan2(dst_rows-old_centre[0],dst_cols-old_centre[1])
R_typical=np.max(centre)
radius=R_typical*((radius.astype(float))/R_typical)**a
#theta=theta*1.0
dst_rows=radius*np.sin(theta)+old_centre[0]
dst_cols=radius*np.cos(theta)+old_centre[1]
#dst_rows=dst_rows/np.max(dst_rows)*dst_rows_max
#dst_cols=dst_cols/np.max(dst_cols)*dst_cols_max
elif transform =='thetascale':
dst_rows_max=np.max(dst_rows)
dst_cols_max=np.max(dst_cols)
radius=(radius.astype(float))**1.25
theta=theta*0.25
dst_rows=radius*np.sin(theta)+centre[0]
dst_cols=radius*np.cos(theta)+centre[1]
elif transform=='sine':
dst_rows = src[:, 1] - np.sin(np.linspace(0, 3 * np.pi, src.shape[0])) * 50
dst_cols = src[:, 0]
dst_rows *= 1.5
dst_rows -= 1.5 * 50
dst = np.vstack([dst_cols, dst_rows]).T
# Calculate the corners of the rotated image
tform = PiecewiseAffineTransform()
tform.estimate(src, dst)
return tform, dst,src, rows, cols,dst_cols,dst_rows
appdir = Path(__file__).parent
app_ui = ui.page_fluid(
ui.layout_sidebar(
ui.sidebar(
ui.input_slider(id="a",label="Parameter",min=-3.0,max=3,value=1.0,step=0.16),
ui.input_select(id="trans",label="Transform",choices=['Identity','Y stretch','Pinch','Fish eye','Shear','Y squish','Radial'],selected=['Pinch']),
ui.input_file(id='input_file',label='Input file',width='1%',button_label='Upload',accept=['.png,.jpg','jpeg'])),
ui.output_plot("plot"),
),
)
def server(input: Inputs, output: Outputs, session: Session):
@reactive.calc
def load_image():
im_index=1#input.d()
#load_image=1
if im_index==1:
image = ski.data.coins()
image_orig=image[-1:0:-1,:]
return image_orig
@render.plot
def plot():
image= load_image()
def parsed_file():
file: list[FileInfo] | None = input.input_file()
if file is None:
return pd.DataFrame()
return imread( # pyright: ignore[reportUnknownMemberType]
file[0]["datapath"])
if input.input_file():
image = parsed_file()
#image=image[-1:0:-1]
if len(image.shape)==3:
im_num_voxels=float(image.shape[0]*image.shape[1])
target_num_voxels=100000.0
target_num_voxels=np.min([target_num_voxels,im_num_voxels])
rescale_factor= target_num_voxels/im_num_voxels
image=rescale(image,rescale_factor,channel_axis=2,anti_aliasing=True)
old_centre=np.array((image.shape[0]/2.0,image.shape[1]/2.0))
fig,ax=plt.subplots(1,2,sharey=True,sharex=True)
# Input parameters
a =float(input.a())
trans=input.trans()
new_image=image
transform=trans
a_i=a
tform,dst,src,rows, cols,dst_cols,dst_rows= ChooseTransform(transform,new_image.shape,a_i,4,old_centre)
# Find corners
corners = np.array([[0, 0], [0, new_image.shape[0]], [new_image.shape[1], 0], [new_image.shape[1], new_image.shape[0]]])
tformed_corners = tform(corners)
minc = tformed_corners.min(axis=0)
maxc = tformed_corners.max(axis=0)
# Find dimensions of transformed box
output_shape = 2*(np.ceil(maxc)[::-1]-np.ceil(minc)[::-1]).astype(int)
# Calculate the translation required to move all points into positive coordinates
min_coords = dst.min(axis=0)
translation = -min_coords
tform_shift = AffineTransform(translation=translation)
# Apply the warp with translation to ensure positive coordinates
output_shape = (int(rows + 2*translation[1]), int(cols + 2*translation[0]))
new_image_trans = warp(new_image, tform_shift.inverse , output_shape=output_shape)
# Define transform on new image
# Define the forward transform and transform the image
tform,dst,src,rows, cols,dst_cols,dst_rows= ChooseTransform(transform,new_image_trans.shape,a_i,30,old_centre)
new_image = warp(new_image_trans,tform.inverse)
# Plot image + transform
ax[0].imshow(image)
ax[0].set_title('Original')
ax[1].imshow(new_image)
ax[1].set_title('Transformed')
fig.subplots_adjust(wspace=0, hspace=0)
fig.tight_layout()
plt.show()
app = App(app_ui, server)
Composite maps
We can build composite maps by using the output image from one transform as the input image for another. In Figure 3 you can explore the effect of combining two transforms successively. This allows for the construction of many interesting final images.
#| standalone: true
#| components: [viewer]
#| viewerHeight: 600
from shiny import App, Inputs, Outputs, Session, render, ui
from shiny import reactive
import numpy as np
import matplotlib.pyplot as plt
import skimage as ski
import pyodide
from skimage.transform import SimilarityTransform
from skimage.transform import warp
from skimage.transform import PiecewiseAffineTransform
from skimage.transform import AffineTransform
from skimage.io import imread
import io
from pathlib import Path
from skimage.transform import resize, rescale
def ChooseTransform(transform,im_shape,a,num_disc_points,old_centre):
rows=im_shape[0]
cols=im_shape[1]
src_cols = np.linspace(0, cols, num_disc_points)
src_rows = np.linspace(0, rows, num_disc_points)
src_rows, src_cols = np.meshgrid(src_rows, src_cols)
src = np.dstack([src_cols.flat, src_rows.flat])[0]
dst_rows = src[:, 1]
dst_cols = src[:, 0]
#['Identity','Y stretch','Pinch','Fish eye','Shear','Y squish','Radial']
# add sinusoidal oscillation to row coordinates
#transform='yscaleDarcy299Fig147'
if transform=='Identity':
dst_rows = src[:, 1]
dst_cols = src[:, 0]
elif transform=='Y stretch':
yscaleparam=a
dst_rows = dst_rows*yscaleparam
dst_cols = src[:, 0]
elif transform=='Pinch': #'yscaleDarcy299Fig151':
sc_factor=a
k_x=sc_factor*((dst_cols-cols/2.0)/cols)**1.0+1.0
dst_rows = k_x*(dst_rows-rows/2.0)+rows/2.0
#dst_cols = src[:, 0]
elif transform=='Fish eye': #'yscaleDarcy299Fig149':
dst_rows = (dst_rows-rows/2.0)*(2.5-a*((dst_cols-cols/2.0)/(cols/2.0))**2.0)+rows/2.0
#dst_cols = (dst_cols-cols/2.0)*(dst_rows-rows/2.0)**2.0+cols/2.0
#dst_cols = src[:, 0]
#dst_cols = src[:, 0]
elif transform=='Shear': #'yscaleDarcy299Fig147':
k_y=-a
dst_cols = dst_cols+k_y*dst_rows
#dst_cols = src[:, 0]
elif transform=='Y squish':
L=np.max(dst_rows)
dst_rows = (np.log(1.0+a*(dst_rows)/L))*L/np.log(2.0)
#dst_cols = src[:, 0]
elif transform=='yscalepower':
L=np.max(dst_rows)
n=a
dst_rows = L*(dst_rows/L)**n
#dst_cols = src[:, 0]
elif transform=='Radial':
dst_rows_max=np.max(dst_rows)
dst_cols_max=np.max(dst_cols)
centre=[cols/2.0,rows/2.0]
radius=np.sqrt((dst_rows-old_centre[0])**2+(dst_cols-old_centre[1])**2)
theta=np.arctan2(dst_rows-old_centre[0],dst_cols-old_centre[1])
R_typical=np.max(centre)
radius=R_typical*((radius.astype(float))/R_typical)**a
#theta=theta*1.0
dst_rows=radius*np.sin(theta)+old_centre[0]
dst_cols=radius*np.cos(theta)+old_centre[1]
#dst_rows=dst_rows/np.max(dst_rows)*dst_rows_max
#dst_cols=dst_cols/np.max(dst_cols)*dst_cols_max
elif transform =='thetascale':
dst_rows_max=np.max(dst_rows)
dst_cols_max=np.max(dst_cols)
radius=(radius.astype(float))**1.25
theta=theta*0.25
dst_rows=radius*np.sin(theta)+centre[0]
dst_cols=radius*np.cos(theta)+centre[1]
elif transform=='sine':
dst_rows = src[:, 1] - np.sin(np.linspace(0, 3 * np.pi, src.shape[0])) * 50
dst_cols = src[:, 0]
dst_rows *= 1.5
dst_rows -= 1.5 * 50
dst = np.vstack([dst_cols, dst_rows]).T
# Calculate the corners of the rotated image
tform = PiecewiseAffineTransform()
tform.estimate(src, dst)
return tform, dst,src, rows, cols,dst_cols,dst_rows
appdir = Path(__file__).parent
app_ui = ui.page_fluid(
ui.layout_sidebar(
ui.sidebar(
ui.input_slider(id="a1",label="Parameter 1",min=-3.0,max=3,value=1.0,step=0.16),
ui.input_slider(id="a2",label="Parameter 2",min=-3.0,max=3,value=1.0,step=0.16),
ui.input_select(id="trans1",label="Transform 1",choices=['Identity','Y stretch','Pinch','Fish eye','Shear','Y squish','Radial'],selected=['Pinch']),
ui.input_select(id="trans2",label="Transform 2",choices=['Identity','Y stretch','Pinch','Fish eye','Shear','Y squish','Radial'],selected=['Pinch']),
ui.input_file(id='input_file',label='Input file',width='1%',button_label='Upload',accept=['.png,.jpg','jpeg'])),
ui.output_plot("plot"),
),
)
def server(input: Inputs, output: Outputs, session: Session):
@reactive.calc
def load_image():
im_index=1#input.d()
#load_image=1
if im_index==1:
image = ski.data.coins()
image_orig=image[-1:0:-1,:]
return image_orig
@render.plot
def plot():
image= load_image()
def parsed_file():
file: list[FileInfo] | None = input.input_file()
if file is None:
return pd.DataFrame()
return imread( # pyright: ignore[reportUnknownMemberType]
file[0]["datapath"])
if input.input_file():
image = parsed_file()
#image=image[-1:0:-1]
if len(image.shape)==3:
im_num_voxels=float(image.shape[0]*image.shape[1])
target_num_voxels=100000.0
target_num_voxels=np.min([target_num_voxels,im_num_voxels])
rescale_factor= target_num_voxels/im_num_voxels
image=rescale(image,rescale_factor,channel_axis=2,anti_aliasing=True)
fig,ax=plt.subplots(1,2,sharey=True,sharex=True)
# Input parameters
a1 =float(input.a1())
a2 =float(input.a2())
trans1 =input.trans1()
trans2 =input.trans2()
trans=[trans1,trans2]
old_centre=np.array((image.shape[0]/2.0,image.shape[1]/2.0))
trans=[trans1,trans2]
a=[a1,a2]
new_image=image
for tranform_i,a_i in zip(trans,a):
transform=tranform_i
tform,dst,src,rows, cols,dst_cols,dst_rows= ChooseTransform(transform,new_image.shape,a_i,4,old_centre)
# Find corners
corners = np.array([[0, 0], [0, new_image.shape[0]], [new_image.shape[1], 0], [new_image.shape[1], new_image.shape[0]]])
tformed_corners = tform(corners)
minc = tformed_corners.min(axis=0)
maxc = tformed_corners.max(axis=0)
# Find dimensions of transformed box
output_shape = 2*(np.ceil(maxc)[::-1]-np.ceil(minc)[::-1]).astype(int)
# Calculate the translation required to move all points into positive coordinates
min_coords = dst.min(axis=0)
translation = -min_coords
tform_shift = AffineTransform(translation=translation)
# Apply the warp with translation to ensure positive coordinates
output_shape = (int(rows + 2*translation[1]), int(cols + 2*translation[0]))
new_image_trans = warp(new_image, tform_shift.inverse , output_shape=output_shape)
# Define transform on new image
# Define the forward transform and transform the image
tform,dst,src,rows, cols,dst_cols,dst_rows= ChooseTransform(transform,new_image_trans.shape,a_i,30,old_centre)
new_image = warp(new_image_trans,tform.inverse)
# Plot image + transform
ax[0].imshow(image)
ax[0].set_title('Original')
ax[1].imshow(new_image)
ax[1].set_title('Composite transformed')
fig.subplots_adjust(wspace=0, hspace=0)
fig.tight_layout()
plt.show()
app = App(app_ui, server)
Suppose we have an image, \(I\), and two mappings, \(f\) and \(g\).
We represent transformation of the image via the first transform as
\[
I'=f \circ I.
\]
Applying the second transform yields \[ I''=g\circ (f \circ I). \]
We might then ask:
- is the final image affected by the order in which you perform the transformations (i.e. is \(f\circ g = g\circ f\))?
- does an inverse mapping exist such that any transformation can be reversed via a further transformation? i.e. for a given \(f\) can we find a \(g\) such that \[ I''=g\circ (f \circ I)=I. \]
By understanding whether such properties hold, we can classify different families of mappings and better understand why particular mappings behave the way that they do.
At Dundee, concepts from geometry are studied in core modules Maths 1A and Maths 1B.
At Level 3 in the module Differential Geometry students study generalisations of 2D mappings to arbitrarily curved spaces.
You can find out more about these modules here.